Сама идея метода главных компонент проста и гениальна. Рассмотрим ее на бытовом уровне. Предположим, что у нас есть последовательность событий. Каждое из них мы описываем через его влияние на сенсоры, которыми мы воспринимаем мир. Допустим, что у нас \(m\) сенсоров, описывающих \(m\) признаков \(p_{1}\cdots p_{m}\). Все события для нас описываются векторами \(x\) размерности \(m\). Каждый компонент \(x_{i}\) такого вектора указывают на значение соответствующего \(i\)-го признака. Все вместе они образуют случайную величину X. Эти события мы можем изобразить в виде точек в \(m\)-мерном пространстве, где осями будут выступать наблюдаемые нами признаки.
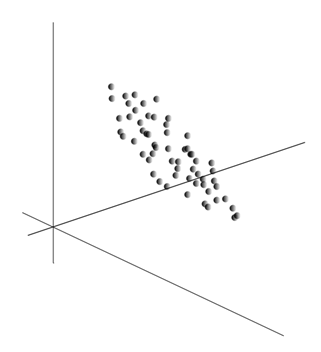
Усреднение значений \(x\) дает математическое ожидание случайной величины X, обозначаемое, как E(X). Если мы отцентрируем данные так, чтобы E(X)=0, то облако точек будет сконцентрировано вокруг начала координат.
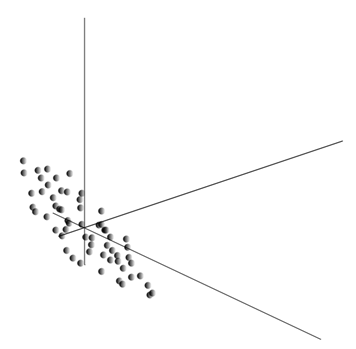
Это облако может оказаться вытянутым в каком-либо направлении. Перепробовав все возможные направления, мы можем найти такое, вдоль которого дисперсия данных будет максимальной.
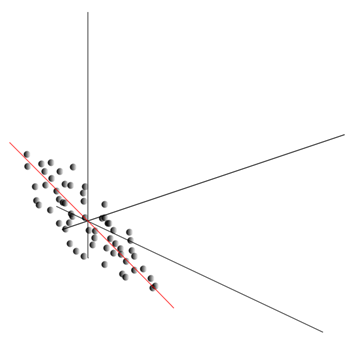
Так вот, такое направление соответствует первой главной компоненте. Сама главная компонента определяется единичным вектором, выходящим из начала координат и совпадающим с этим направлением.
Далее мы можем найти другое направление, перпендикулярное первой компоненте, такое, чтобы вдоль него дисперсия также была максимальной среди всех перпендикулярных направлений. Найдя его, мы получим вторую компоненту. Затем мы можем продолжить поиск, задавшись условием, что искать надо среди направлений, перпендикулярных уже найденным компонентам. Если исходные координаты были линейно независимы, то так мы сможем поступить \(m\) раз, пока не закончится размерность пространства. Таким образом, мы получим \(m\)взаимоортогональных компонент \(q\), упорядоченных по тому, какой процент дисперсии данных они объясняют.
Естественно, что полученные главные компоненты отражают внутренние закономерности наших данных. Но есть более простые характеристики, также описывающие суть имеющихся закономерностей.
Предположим, что всего у нас n событий. Каждое событие описывается вектором \(x_{i}\). Компоненты этого вектора:
\[x_{i}=(x_{i1}\cdots x_{im})^{T}\]
Для каждого признака \(p_{k}\) можно записать, как он проявлял себя в каждом из событий:
\[p_{k}=(x_{1k}\cdots x_{nk})^{T}\]
Для любых двух признаков, на которых строится описание, можно посчитать величину, показывающую степень их совместного проявления. Эта величина называется ковариацией:
\[cov(p_{i},p_{j})=\frac{1}{n}\sum_{k=1}^{n}(x_{ki}-\bar{p}_{i})(x_{kj}-\bar{p}_{j})\]
Она показывает, насколько отклонения от среднего значения одного из признаков совпадают по проявлению с аналогичными отклонениями другого признака. Если средние значения признаков равны нулю, то ковариация принимает вид:
\[cov(p_{i},p_{j})=\frac{1}{n}\sum_{k=1}^{n}x_{ki}x_{kj}\]
Если скорректировать ковариацию на среднеквадратические отклонения, свойственные признакам, то мы получим линейный коэффициент корреляции, называемый еще коэффициентом корреляции Пирсона:
\[r(p_{i},p_{j})=\frac{cov(p_{i},p_{j})}{\sigma (p_{i})\sigma (p_{j})}\]
Коэффициент корреляции обладает замечательным свойством. Он принимает значения от -1 до 1. Причем 1 означает прямую пропорциональность двух величин, а -1 говорит об их обратной линейной зависимости.
Из всех попарных ковариаций признаков можно составить ковариационную матрицу \(R\), которая, как несложно убедиться, есть математическое ожидание произведения \(XX^{T}\):
\[R=E(XX^{T})\]
Будем далее полагать, что наши данные отнормированы, то есть имеют единичную дисперсию. В этом случае корреляционная матрица совпадает с ковариационной матрицей.
Так вот оказывается, что для главных компонент \(q\) справедливо:
\[Rq=\lambda q\]
То есть главные компоненты, или, как еще их называют, факторы являются собственными векторами корреляционной матрицы \(R\). Им соответствуют собственные числа \(\lambda\). При этом, чем больше собственное число, тем больший процент дисперсии объясняет это фактор.
Зная все главные компоненты \(q\), для каждого события \(x\), являющегося реализацией X, можно записать его проекции на главные компоненты:
\[a_{j}=q_{j}^{T}x\]
Таким образом, можно представить все исходные события в новых координатах, координатах главных компонент:
\[x=Qa=\sum_{j=1}^{m}a_{j}q_{j}\]
Вообще различают процедуру поиска главных компонент и процедуру нахождения базиса из факторов и его последующее вращение, облегчающее трактовку факторов, но так как эти процедуры идеологически близки и дают похожий результат, будем называть и то и другое факторным анализом.
За достаточно простой процедурой факторного анализа кроется очень глубокий смысл. Дело в том, что если пространство исходных признаков – это наблюдаемое пространство, то факторы – это признаки, которые хотя и описывают свойства окружающего мира, но в общем случае (если не совпадают с наблюдаемыми признаками) являются сущностями скрытыми. То есть формальная процедура факторного анализа позволяет от явлений наблюдаемых перейти к обнаружению явлений, хотя непосредственно и невидимых, но, тем не менее, существующих в окружающем мире.
Можно предположить, что наш мозг активно использует выделение факторов как одну из процедур познания окружающего мира. Выделяя факторы, мы получаем возможность строить новые описания происходящего с нами. Основа этих новых описаний – выраженность в происходящем тех явлений, что соответствуют выделенным факторам.
Немного поясню суть факторов на бытовом уровне. Предположим, вы менеджер по персоналу. К вам приходит множество людей, и относительно каждого вы заполняете определенную форму, куда записываете разные наблюдаемые данные о посетителе. Просмотрев потом свои записи, вы можете обнаружить, что некоторые графы имеют определенную взаимосвязь. Например, стрижка у мужчин будет в среднем короче, чем у женщин. Лысых людей вы, скорее всего, встретите только среди мужчин, а красить губы будут только женщины. Если к анкетным данным применить факторный анализ, то именно пол и окажется одним из факторов, объясняющим сразу несколько закономерностей. Но факторный анализ позволяет найти все факторы, которые объясняют корреляционные зависимости в наборе данных. Это значит, что кроме фактора пола, который мы можем наблюдать, выделятся и другие, в том числе и неявные, ненаблюдаемые факторы. И если пол явным образом будет фигурировать в анкете, то другой важный фактор останется между строк. Оценивая способность людей связано излагать свои мысли, оценивая их карьерную успешность, анализируя их оценки в дипломе и тому подобные признаки, вы придете к выводу, что есть общая оценка интеллекта человека, которая явным образом в анкете не записана, но которая объясняет многие ее пункты. Оценка интеллекта – это и есть скрытый фактор, главная компонента с высоким объясняющим эффектом. Явно мы эту компоненту не наблюдаем, но мы фиксируем признаки, которые с ней коррелированы. Имея жизненный опыт, мы можем подсознательно по отдельным признакам формировать представление об интеллекте собеседника. Та процедура, которой при этом пользуется наш мозг, и есть, по сути, факторный анализ. Наблюдая за тем, как те или иные явления проявляются совместно, мозг, используя формальную процедуру, выделяет факторы, как отражение устойчивых статистических закономерностей, свойственных окружающему нас миру.